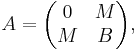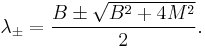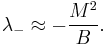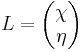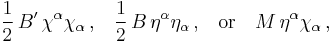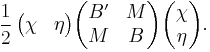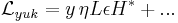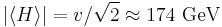Seesaw mechanism
In theoretical physics, the seesaw mechanism is a mechanism within grand unification theory, and in particular in theories of neutrino masses and neutrino oscillation, where it can be used to explain the smallness of observed neutrino masses relative to those of quarks and leptons.
There are several varieties commonly referred to as type 1 seesaw, type 2 seesaw etc. The simplest version, type 1, requires as additional assumptions to the standard model only two or more right-handed neutrino fields,[1] and the existence of a very large mass scale in the theory which can for example be the scale of grand unification.
Contents |
Type 1 seesaw
This model produces a light neutrino, corresponding to the three known neutrino flavors, and a very heavy, undiscovered sterile neutrino, which has possibly been detected.[2]
The mathematics behind the seesaw mechanism is the following fact: the 2×2 matrix
where  is much larger than
is much larger than  , has the following eigenvalues:
, has the following eigenvalues:
The larger eigenvalue is approximately equal to  while the smaller eigenvalue is approximately equal to
while the smaller eigenvalue is approximately equal to
Therefore, M is the geometric mean of B and λ−, up to the sign. In other words, the determinant equals λ+λ− = −M2. If one of the eigenvalues goes up, the other goes down, and vice versa. This is the reason why the name seesaw was given to the mechanism.
This mechanism is used to explain why the neutrino masses are so small.[3][4][5] The matrix A is essentially the mass matrix for the right-handed neutrino. The Majorana mass  is comparable to the GUT scale and M, the Dirac mass, is of order of the electroweak scale. The smaller eigenvalue then leads to a very small neutrino mass comparable to 1 eV which qualitatively agrees with the experiments. Such an agreement may be interpreted as an experimentally confirmed qualitative prediction of Grand Unified Theories.
is comparable to the GUT scale and M, the Dirac mass, is of order of the electroweak scale. The smaller eigenvalue then leads to a very small neutrino mass comparable to 1 eV which qualitatively agrees with the experiments. Such an agreement may be interpreted as an experimentally confirmed qualitative prediction of Grand Unified Theories.
Field Theory Background
The 2×2 matrix A arises in a natural manner within the standard model by considering the most general mass matrix allowed by gauge invariance of the standard model action, and the corresponding charges of the lepton- and neutrino fields. Let the Weyl spinor χ be the neutrino part of a left-handed lepton isospin doublet
as it is present in the minimal standard model without neutrino masses, and let η be a postulated right-handed neutrino Weyl spinor which is a singlet under weak isospin. There are now three ways to form Lorentz covariant mass terms, giving either
and their complex conjugates, which can be written as a quadratic form,
Since the right-handed neutrino spinor is uncharged under all standard model gauge symmetries, B is a free parameter which can in principle take any arbitrary value. The parameter M is forbidden by electroweak gauge symmetry, and can only appear after its spontaneous breakdown through a Higgs mechanism. In particular, since χ ∈ L has weak isospin ½ like the Higgs field H, and χ has weak isospin 0, the mass parameter M can be generated from Yukawa interactions with the Higgs field,
This means that M is naturally of the order of the vacuum expectation value of the standard model Higgs field,
if the dimensionless Yukawa coupling is y ≈ 1. It can be chosen smaller consistently, but extreme values y ≫ 1 can make the model nonperturbative. The parameter B' on the other hand, is completely forbidden, since no singlet under weak hypercharge and isospin can be formed using these objects. This is the origin of the pattern and hierarchy of scales of the mass matrix A within the "type 1" seesaw mechanism. The exact size of B can be explained in the context of grand unification. In such models, enlarged gauge symmetries may be present which initially force B = 0 in the unbroken phase, but generate a nonvanishing value B ≈ MGUT around the scale of their spontaneous symmetry breaking.
See also
References
- ^ It is possible to generate two light but massive neutrinos with only one right-handed neutrino, but the resulting spectra are generally not viable.
- ^ Popular Science - Fermilab Experiment Hints At Existence of Brand-New Elementary Particle
- ^ M. Gell-Mann, P. Ramond and R. Slansky, in Supergravity, ed. by D. Freedman et al., North Holland (1979).
- ^ T. Yanagida (1980). "Horizontal Symmetry and Masses of Neutrinos". Progress of Theoretical Physics 64 (3): 1103–1105. doi:10.1143/PTP.64.1103.
- ^ R. N. Mohapatra, G. Senjanovic (1979). "Neutrino Mass and Spontaneous Parity Nonconservation". Phys. Rev. Lett. 44 (14): 912–915. Bibcode 1980PhRvL..44..912M. doi:10.1103/PhysRevLett.44.912.